Efficiency of uranium use (Sustainability Assessment)

This page is the "Appendix IV" to Environmental Impact from Depletion of Resources

This appendix presents examples of the end uses of uranium (normalized by energy delivered in GW·a) in a simple NES consisting of a nuclear power plant with an open (once through) uranium fuel cycle analysed with the NEST code described in Ref..

Description of the nuclear energy system

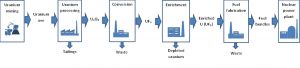
Figure 1 illustrates the mass flow of front end facilities of an NES starting with mining and ending with the nuclear power plant.

FIG. 1. Fuel production chain for a light water reactor using uranium fuel in an open fuel cycle.

The characteristics of the individual nuclear fuel cycle facilities that are typical for a current NES with an open fuel cycle are presented in Table 8 (input data necessary for calculation).

Table 1. Characteristics of individual fuel cycle facilities in a typical current nuclear energy system

Front end fuel cycle stages and nuclear power plant operation	Parameter	Name	Value
Mining and processing	U-235 concentration in natural isotopes blend (%/100)	εF	0.00711
	Losses at extraction (%/100)	l1	0.20*
Conversion	Losses (%/100)	l2	0.005
Enrichment	U-235 concentration in fuel (%/100)	εP	0.04
	U-235 concentration in depleted uranium (%/100)	εT	0.0025
	Losses (%/100)	l3	0
Fuel fabrication	Losses (%/100)	l4	0.01
Nuclear power plant (energy conversion)	Unloaded fuel average burnup (MW·d/kg)	Q	45
	Nuclear power plant net thermal efficiency (%/100)	η	0.32

* - The lower margin of a range provided in Ref. (20–35% depending on the technology) is used for this example. ‘0.20’ corresponds to open pit mining with conventional milling.

Material balance of the nuclear energy system

A detailed algorithm of the material balance calculation for different options of the fuel cycle, including the front end of a once through fuel cycle is described in Appendix II of the INPRO methodology manual on economics.
The equation describing the link between the mass of heavy metals at different stages of the front end of the fuel cycle (HMk),

${\mathrm {HM} }_{k}=\prod _{j=k}^{N_{\ stages}}{\mathrm {HMI} }_{j}^{j+1}\cdot \left(1+l_{j}\right),(1)$

can be easily converted into a formula for the amount of natural uranium spent on the production of an electricity unit. Here, HMI_j^j+1 is the quantity of heavy metal necessary at stage j to produce 1 kg of fuel at the next stage (j+1) without accounting for losses (i.e. in an ‘ideal’ case); l_j is the loss of uranium during processing at every stage of the front end (e.g. j=2 losses at uranium conversion); all values are input data to NEST.
The equation estimating the amount of natural uranium necessary to produce 1 GW·a of electricity in a once through fuel cycle (HM₀) is the following:

${\rm {HM}}_{0}={\frac {365\times {10}^{3}\cdot {\frac {\varepsilon _{P}-\varepsilon _{T}}{\varepsilon _{F}-\varepsilon _{T}}}\cdot \left(1+l_{1}\right)\cdot \left(1+l_{2}\right)\cdot \left(1+l_{3}\right)\cdot \left(1+l_{4}\right)}{\eta \cdot Q}},(2)$

where 365 × 10³ is a coefficient converting GW·a into MW·d, and the rest of parameters are described in Table 1 (for simplicity, the first core fuel and reload fuel are not differentiated between here).
Numerical calculation based on the input data in Table 1 yields that approximately 2.5 × 10⁵ kg of natural uranium is necessary to produce 1 GW·a of electricity. For completeness, it should be mentioned that such a result can be obtained not just by using NEST algorithms, and the INPRO assessors may use other tools, e.g. NFCSS developed by the IAEA and available on the IAEA web site.
Thus, the NES retrieves 34.9 GW·h from 1 tU. This value of 34.9 GW·h/tU corresponds to the value of U₀ defined in criterion CR1.4.

Sensitivity of the end use of uranium in the nuclear energy system

By looking at Table 1 (characteristics of NES facilities), it is obvious how the efficiency of the NES could be increased: firstly by reducing the losses in the fuel cycle facilities, i.e. in the processing, conversion and fuel fabrication facility, and by reducing the enrichment in the tailings of the enrichment facility, i.e. in the depleted uranium; and secondly, by increasing the nuclear power plant’s thermal efficiency and average burnup of the nuclear fuel to be unloaded.
In Table 2, the sensitivities of the characteristics of the NES fuel cycle facilities to increase the efficiency of the uranium end use are presented. In the base case, the NES end use of natural uranium amounts to 251.1 tU to generate 1 GW·a of electricity. Table 2 presents the change of the NES end use of uranium in the cases when the losses of uranium in the fuel cycle facilities are decreased by 10% and 20%.

Table 2.Change of natural uranium end use in nuclear energy systems by reduction of losses in the nuclear fuel cycle facilities

Fuel cycle stages	Base case losses (%/100)	Reduction by 10%			Reduction by 20%
		Losses (%/100)	Uranium end use (tU)	Reduction of U end use (tU)	Losses (%/100)	Uranium end use (tU)	Reduction of U end use (tU)
Processing	0.20	0.18	247.0	4.1	0.16	242.8	8.3
Conversion	0.005	0.0045	251.0	0.1	0.004	250.9	0.2
Enrichment	0.0025 (tails assay)	0.00225	239.8	11.3	0.002	229.6	21.5
Fuel fabrication	0.1	0.009	250.9	0.2	0.008	250.6	0.5

Table 3 presents the sensitivities of the characteristics of the nuclear power plant with regard to the end use of natural uranium. The influences of two characteristics are studied, namely, the thermal efficiency of the plant and the (core average) burnup of the nuclear fuel.

Table 3.Change of natural uranium end use in nuclear energy systems by increasing thermal efficiency and burnup in the nuclear power plant

Nuclear power plant parameter	Base case value	Increase by 10%			Increase by 20%
		Parameter value	Uranium end use (tU)	Reduction of uranium end use (tU)	Parameter value	Uranium end use (tU)	Reduction of uranium end use (tU)
Thermal efficiency	0.32 %/100	0.352 %/100	228.3	22.8	22.8 0.384 %/100	209.3	41.8
Average burnup	45 MW·d/kg	49.5 MW·d/kg	228.3	22.8	54 MW·d/kg	209.3	41.8

A comparison of the results in Table 1 with Table 2 indicates that the highest relative increase of efficiency (or reduction) of natural uranium end use in the NES can be achieved by an increase of thermal efficiency of the power plant or by an increase of burnup in the fuel followed by a reduction of the tails assay in the enrichment facility.

See also

• Appendix I
• Appendix II
• Appendix III

	[ + ] Assessment Methodology
Areas of INPRO Sustainability Assessment Overview • Economics • Safety (Nuclear Reactors) • Safety (NFCF) • Waste management • Environmental Impact on Stressors • Environmental Impact from Depletion of Resources • Infrastructure Requirements Basic Principle • User requirements • Criteria